不管是在生活中,还是在网上,时空都是我们喜欢讨论的一个话题,网上也是各种关于空间的科普文章,但很多概念混乱逻辑错误,看得大家云里雾里不知所云。这里我尝试以自己丁点的数学知识,给大家讲一讲空间与纬度。有错误希望大家批评指正。

一.N维空间与线性代数
理工科出身的都在大学里学习过线性代数,如果还有印象,一定还记得什么行列式和矩阵,对于那些奇奇怪怪的运算规则,很多老师却不讲其所以然,一句就是这么规定的应付了事,更多的是在讲解题技巧。同学们学得更是辛苦,死记硬背应付过考试后就忘到九霄云外了,只有少部分同学在以后的学习和专业中才发现线性代数原来这么有用。

线性代数
简单讲线性代数是研究线性对象(向量)在线性空间中的线性运动(线性变换),而矩阵就是对这种线性变换的一种描述。
第一个概“念线性空间”,数学上的空间首先它是集合中的一种,其次这个空间(集合)中有很多(其实是无穷多个)对象组成,所有这些对象之间存在相对关系并且可以定义度量,譬如长度和角度,最后这个空间可以容纳运动。所以线性空间就是向量(行列式)的集合,我们可以选定一个基,建立坐标系,定义长度或者角度,在这个线性空间里可以用矩阵来表示向量的线性运动(变换)。
这里又涉及的一个概念“基”,什么是“基”呢?简单粗暴地讲就是坐标系,这个坐标系有几根坐标轴,那么这个线性空间就是几维的。我们怎么在线性空间里找到一组基呢?如果一组向量是彼此线性无关的话,那么它们就可以成为度量这个线性空间的一组基。如果我们在这个线性空间里找到N组向量线性不相关,每个向量又是N列的行列式,也是N*1的矩阵)那么这个N*N(非奇异)矩阵就是这个线性空间的一组基,其中每一个向量都躺在一根坐标轴上,并且成为那根坐标轴上的基本度量单位(长度1),我们也把这个线性空间称为N维的线性空间。
所以在线性空间里是可以有N个维度,N可以是任意自然数(1,2,3,...),关键点是每个维度彼此线性不相关。
大家可以注意到这个坐标系是可以任意建立,只要是线性不相关的一组向量就可以,那么就带来一个现象,对于A点到B点的运动(变换),因为坐标系的不同,描述这一变化的矩阵也不相同,但他们描述的却又是同一个变化,那么在两个不同坐标系下描述同一向量变换的两个矩阵就是相似矩阵。说到这里学过的同学是不是有点回忆起这个概念了,原来相似矩阵是这么来的,是有它的空间意义的。
对于没有学过线性代数的同学,可能不好理解。举一个线性代数在实际生活中的应用:机械手臂怎么运动的?控制机械手臂的运动的程序就是在计算矩阵(矩阵的左乘,右乘等等),这就是用线性空间的数学方法来描述三维空间中的机械臂(向量)从A点运动到B点的运动(矩阵)。

机器人手臂
线性空间是比较基础的一种空间,从上面的例子可以看到它可以运用到三维的几何空间,它还可以用到4*4的仿射空间,计算机图形学用的就是这个4维仿射空间。
再强调一下成为纬度的关键特性就在于纬度之间的互不相关性。在物理的研究上也并不是只有空间的长宽高三个几何维度,密度,质量,以及各种不相关的物理特性,比如颜色都可以成为研究该对象的一个纬度,有了这些维度一样可以借助线形代数的数学方法了。
下面我们再讲一下几何空间上的维度。
二.几何空间的维度
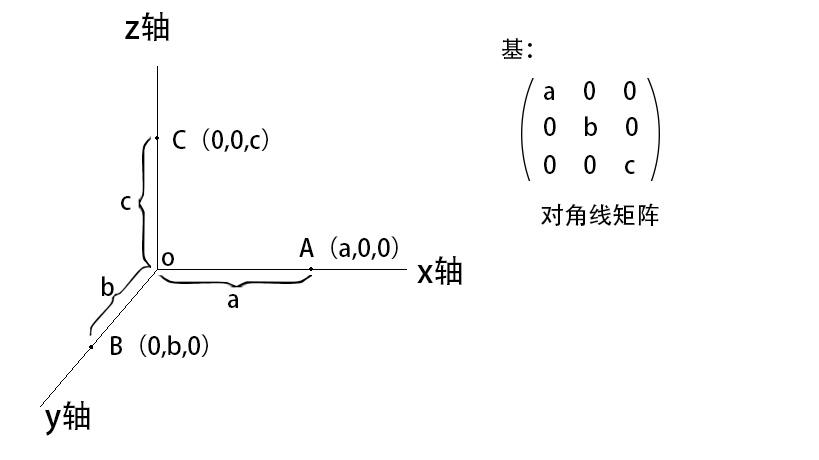
三维坐标系
以我们熟悉的三维欧几里德空间为例,三个维度分别是长宽高,那么他们几何上的不相关特性是怎样的呢?它们的不相关性体现为互相垂直。为什么呢?我们可以看到任何在x轴上任意点A在y轴和z轴的坐标值都是0,坐标为(a,0,0)其他轴上的点也是一样,在另外两个轴上的坐标值都是0,譬如y轴上的B点坐标为(0,b,0),z轴上的点C坐标为(0,0,c)。所以几何上的不相关就是垂直,坐标轴上任意的一个点在其它坐标轴上的分量都是0。根据上面线性空间的知识我们可以看到每个点的坐标都是一个行列式,也是从坐标原点开始的一个向量,而这三个坐标轴上的三个点坐标也构成了一个3*3的矩阵,所以也是一个线性不相关的“基”。从这个意义上说欧几空间是线性空间中的一种。
这就是我们生活中接触到的长宽高的三维欧几里德几何空间。
三.四维时空
在研究我们所在的空间的时候,爱因斯坦这个牛人发现光用长宽高这个三个几何纬度并不能很好地解释我们所处的空间,必须要加上另一个维度,就是与其他三个几何维度互不相关的非几何特性--时间。于是就有了我们所听到的四维时空:三个空间维度加上时间纬度。有人把时间维度称为伪纬度,我认为这是不正确的。并不是只有几何的维度才是维度。
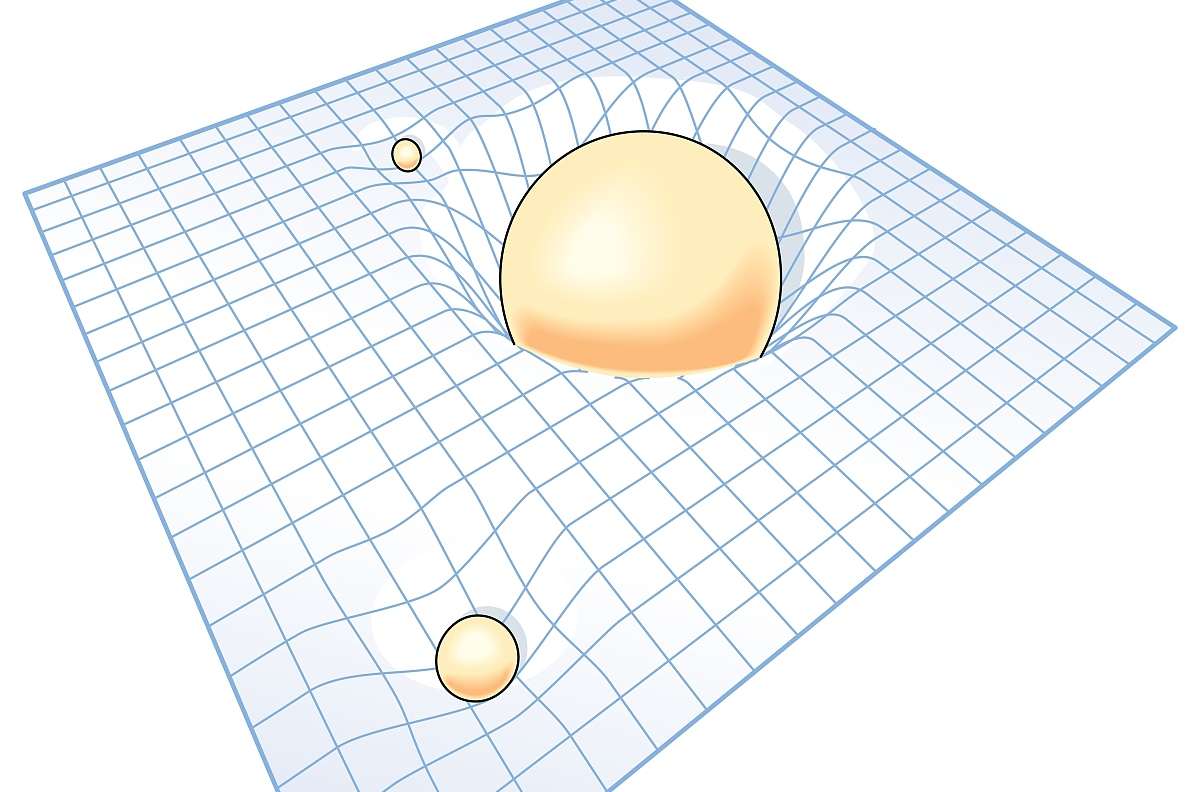
那为什么在研究现实空间的时候必须加上时间维度呢?因为不同空间的时间可能是不一样的,当我们研究某个具体空间时,必须研究这个空间的时间。按照爱因斯坦的广义相对论,每个有质量的物体都会扭曲周围的时空。注意扭曲的并不仅仅是空间,同样还有时间。科学家已经通过实验证实地球外太空的时间比地球表面的时间慢一丢丢。同理太阳表面的时间和我们地球表面时间肯定也是不一样的,因为太阳的质量比地球大的多。我国古代的神话故事里也有天上一天,地下一年的说法,不知道这是不是只是一个巧合。
四.高维空间和11维空间的由来。
前面我们讲了,几何上的不相关性就是垂直,在一个二维平面上x轴垂直y轴,x轴上的点在y轴上没有分量,三维空间里,三个坐标轴也是互相垂直。所以四维空间的第四根坐标轴也是必须和x y z这三个坐标轴互相垂直。显然这第四根坐标轴不存在于三维空间内,所以我们无法看到。
那么高维空间到底存不存在呢?十一维空间又是怎么来的呢?

爱因斯坦的广义相对论准确描述了宇宙宏观世界,最近的天文现象,以及第一次拍到的宇宙中黑洞照片等等都再次证实了广义相对论的正确性。但是广义相对论却无法解释量子力学。
人们在研究量子力学时,发生了令人无法解释的现象,在计算量子微观世界里的概率问题时,概率居然出现了负数,还出现了大于1的结果。学过统计和概率论的都知道,概率处于0到1之间,0表示绝对不可能发生,1表示必然发生,怎么可能出现负数和大于1的数呢?
然后有科学家发现如果只是在三维世界中就会发生这种问题,但是把问题放到高维世界中,这个概率问题就完美的处在了0到1之间。通过计算这个高维是25维。这是弦理论。
然后弦理论进一步升级到了超弦理论(以及统一多种超弦理论的M理论)。按照狭义相对论,光子的速度是不变的,光子之所以按光速运动,因为它的质量是0,所以它的能量也是0。但是按照光子的最低能量加上它的振动能量就是光子的总能量这个公式来计算,在三维空间中计算出光子的能量并不为0,而只有当维度为10的时候,代入数学公式中计算出光子的能量为0。所以就有10维的几何维度加上时间维度成为11维的时空。
我们可以理解为光子的振动并不仅仅在我们看到的三维空间中,还有我们看不到的高维中,所以能量在不同的维度上抵消后光子的总能量为0。
因为超弦理论统一了广义相对论和量子力学,也统一了最基本的四种力(引力、电磁力、弱力和强力),所以它是目前大统一理论的最佳候选之一。
但超弦理论依然还有漏洞,所以这个结论并没有被完全证实。我们可以假设光子是不是也有进不去的更高维空间呢?
五.关于平行宇宙

平行宇宙
我们在平面上任意画一条线,可以画出无穷多与之平行的平行线,这些线都处在这个平面中,我们把这个二维平面升维到三维空间中,可以找到无穷多与之平行的平面,这些平面都在这个三维空间中。
那么只要我们所处的这个三维宇宙空间真的是在更高维的空间中,那么可以推理同样存在无数个与我们这个宇宙空间平行的空间。
那么存在平行空间,那么另一个平行空间就必然有银河系,有太阳系,有地球,甚至还有另一个你?这在逻辑上是不成立的,平行的只是空间,而不是空间里的每个物体。譬如你在一条平行线上画一个红点,难道其它平行线都出线一个红点?平行的只是线而已,它们仍然是相对独立的。但平行空间彼此就毫无影响吗?这也不尽然,假设平面内有根直线与所有平行线相交并打个结,我们向下拉动这根线,所有的平行线都往下弯曲一个弧度,但他们仍然是平行的。所以如果存在同时存在或者能跨越高低维度空间的物质或者能量就能对平行空间施加影响。我们假设光子就是可以同时存在或者能穿越高低维空间的,那么光子在我们这个三维空间能量是正,那在其它维的空间中能量就可能为负,所以也许存在这某种跨纬度的能量守恒。
以上就是我对一些容易混淆的空间和维度概念的一个梳理,有不对的地方请批评指正。